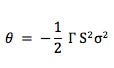What determines an option holder's daily P/L? Part 2
Level 1 - Zero to Options Hero - Wrapping up the explanation of the Greeks and how they relate to the daily P/L of an option
In Part 1 of this post, we went over the concepts of delta equivalence and gamma, and how they relate to understanding the P/L of a long options position. Let’s move to the next step! By the end of this post we should be able to understand the main drivers of an option positions P/L both from one day to the next and also since the inception of the trade.
Vega and Vega P/L
As described in the first post of this series, the price of an option is directly related to the market’s expectation of the future volatility of the underlying asset. So if I buy an option on Day 1, and then the market raises its expectation of the future volatility of the underlying asset (otherwise known as ‘bidding up the option price’ or ‘bidding up the implied volatility’), the option I bought will be worth more. In other words, the buyer would be able to sell the option back into the market at a higher price, all else equal (assuming no passage of time or move in the underlying asset’s price).
Great, but how do we quantify this exactly? Or to put it another way, if the implied volatility in the market for this option goes from 20% to 21% annualized, how much money has the option holder made? This is where the concept of Vega comes in. Vega can be thought of as a $ multiplier, (or coefficient/partial derivative to the math whizzes out there!) of the option price to a 1% move higher in the implied volatility. Therefore, the Vega P/L is: Vega * (ImpliedVol_now - ImpliedVol_inception). It can also be expressed as a daily Vega P/L:
Vega * (ImpliedVol at Close - ImpliedVol at Open).
To use our example of a 1 month $300 call on TSLA when the stock price is $258 (current as of June 13 2023), the vega for this option is approximately $0.22 per share or $22 per contract (remember that each option contract can be exercised for 100 shares of the underlying stock).1 This means that if the implied volatility of TSLA went from its current level (say 60%) up 1% (or what traders refer to as 1 vol point) to 61%, the buyer of 1 option contract would gain a P/L of +$22.
Theta and Time Decay
Theta, otherwise known as time decay, is the change in the price of the option over one trading day, assuming that the stock price does not move at all during the day and the implied volatility also stays unchanged throughout the day. The reason that it is referred to as decay is that in the vast majority of cases the theta of long European options (European here refers to the fact that they can only be exercised at maturity) is negative — that is, the price of the option goes down over time all else equal. For those interested, here is a good explanation of the cases when the theta of a long European option can be positive (it is only in the case when the option is deeply in the money).
There is a neat and easy to remember relationship that ties together the option’s implied volatility, gamma, and theta which pro traders would definitely have memorized.
Now you may ask what exactly am I supposed to do with this formula? Well, there are a couple of interesting takeaways here.
Theta is directly proportional to the gamma with a negative sign. This can be thought of as the gamma theta tradeoff — that is, the more gamma you want to have in your portfolio, the theta will counteract that linearly.
Theta is directly proportional to the square of the implied volatility with a negative sign. So the options in your portfolio that have double the implied volatility of others will have 4x the theta or time decay. This can be useful when it comes to looking at relative value cross-asset class or spread trades in options or when looking at calendar spread trades.
Now we can take the daily P/L breakdown equation from part 1 of this series, and add in the effects of Vega and Theta:
Long Call Option P/L Over 1 Day:
Delta*(StockPrice at Close - StockPrice at Open)
+ 1/2 * Gamma * (StockPrice at Close - StockPrice at Open) ^ 2
+ Vega * (ImpliedVol at Close - ImpliedVol at Open)
+ Theta
That’s all for this post, let me know if any questions! There will be a part 3 coming up which will wrap up the loose ends of the option daily P/L series, but these are the most important parts to understand.
For readers who would like to send us a tip and remain free subscribers for now, we have a tip jar at buymeacoffee.com/optionsnerds - Thanks for your support!