Giving Intuition to the Black-Scholes formula

Level 2 - Intermediate Vol Trader - An intuitive understanding

As mentioned previously, the Black-Scholes formula is the market standard for pricing options. Now we will go into some more detail on the formula and help develop an intuition for why it looks the way it does. Let’s go!

The Black-Scholes formula states that the price of a Call option ( C ) is:

Where N is the standard normal cumulative distribution function:

\(N(z) = \int_{-\infty}^{z} \frac{1}{\sqrt{2\pi}} e^{-\frac{x^2}{2}} \, dx \)

Wow! This sounds way too complicated.

Not to worry. Let’s attack this from first principles.

According to the definition of the call option payoff:

\(Price\ of\ a\ call\ option\ at\ expiry = max(0, S_T-K)\)

which is effectively the same as saying:

\(C_T = max(0, S_T - K) = \begin{cases} S_T - K & \text{if } S_T > K \\ 0 & otherwise \\ \end{cases}\)

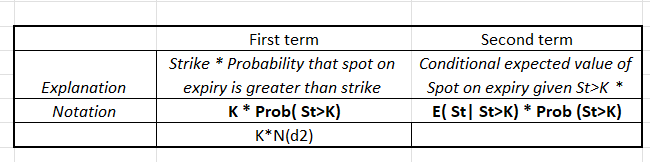
Can we split the above statement into two parts? Yes! It would look like:

\(C^1_T = \begin{cases} - K & \text{if } S_T \geq K \\ 0 & otherwise \\ \end{cases}\)

and

\(C^2_T = \begin{cases} S_T & \text{if } S_T \geq K \\ 0 & otherwise \\ \end{cases}\)

In other words,

\(C^1_T = K * Prob(S_T > K)\)

or

Strike * Probability that spot at expiry is greater than strike

or K*N(d2) where N(d2) is probability that Spot at expiry is greater than strike.

(Hold your horses, I will come back to explaining N(d2) shortly)

Moving on to the second term in the decomposition:

\(C^2_T = E[S_T|S_T>K] * Prob(S_T > K)\)

or:

The conditional expected value of Spot on expiry given St>K * Probability that spot on expiry is greater than strike

Lets summarize what we have learned so far:

Now we need to convert a future payoff to present. Taking present values (multiplying by the discount factor exp(-r*T)) :

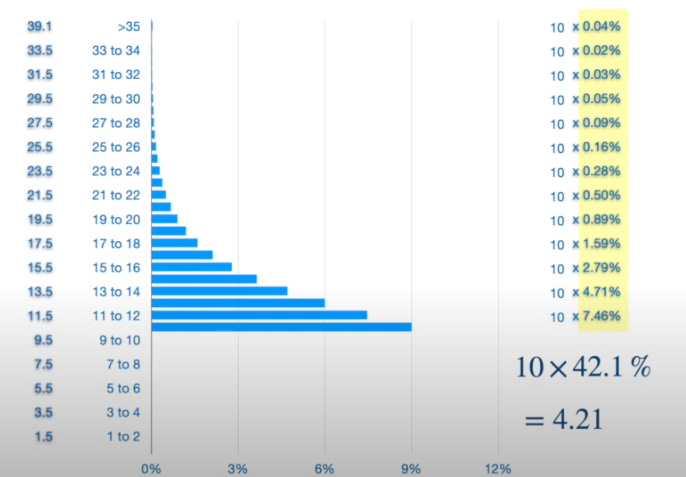
Assume the stock price today is $10 and strike price is $10.

The picture below can be viewed as the:

“truncated average of stock price truncated above the strike price”

See the below chart:

And this one:

Picture credit: quantpie

The above 2 snapshots essentially decompose the Black-Scholes equation for you.

Therefore, the price of the option above is: $5.80 - $4.21= $1.59.

For readers who would like to send us a tip and remain free subscribers for now, we have a tip jar at www.buymeacoffee.com/optionsnerds - Thanks for your support!